Кузнецов А.Л., д.т.н., профессор, ФГБОУ ВО «ГУМРФ имени адмирала С.О. Макарова»;

Сперанская Я.А., инженер кафедры портов и грузовых терминалов ФГБОУ ВО «ГУМРФ имени адмирала С.О. Макарова»

Введение

На любом рынке для каждой товарной группы непрерывно происходит выравнивание спроса и предложения. Не является исключением и фрахтовый рынок, где товаром фактически является провозная способность флота [1-3]. По сути, рынок представляет собой сложную динамическую систему, состояние которой характеризуется состоянием множества элементов, описываемых изменяющимися во времени параметрами.

В качестве элементов рассматриваемой системы могут рассматриваться суда, находящиеся в эксплуатации, заказанные для постройки, вводимые в строй и списываемые [4]. Все элементы, в свою очередь, определяются параметрами, одни из которых являются управляемыми, другие – случайными. Вследствие влияния последних поведение рассматриваемой динамической системы в целом носит случайный характер.

На систему действуют как внутренние силы, определяемые взаимодействием между элементами, так и внешние – возникают вследствие воздействия на нее любых внешних объектов. Внутренние элементы и взаимосвязи между ними являются предметом рассмотрения в данной статье, внешние объекты и их воздействие на систему рассматриваются как заданные [5].

Методы и материалы

Для изучения основных действующих факторов и, соответственно, основных свойств этой системы упростим рассматриваемую модель рынка судоходства до ограниченного числа элементов, перечисленных ранее в настоящей работе [6].

Пусть каждый элемент системы задан соответствующей переменной и характеризует состояние модели в момент времени [t]:

1. Спрос на суда D[t]

2. Суда в эксплуатации N[t]

3. Суда в постройке B[t]

4. Заказ на постройку судов O[t]

5. Ввод судов в эксплуатацию L[t]

6. Вывод судов на слом S[t]

Очевидно, что с течением времени исследуемая динамическая система изменит свое состояние. Таким образом, в момент времени [t+1] система претерпит изменения в соответствии со следующими правилами:

1. D[t] – свободная (управляющая) переменная.

Значения этой независимой переменной характеризует внешние по отношению к исследуемой проблеме факторы, перечисленные ранее в настоящей работе. Иначе говоря, они не будут приниматься во внимание во внутренней нотации рассматриваемой задачи.

2. N[t+1] = N[t] – S[t] + L[t].

Количество судов в эксплуатации уменьшается за счет вывода их из эксплуатации и увеличивается за счет ввода судов в строй.

3. B[t+1] = B[t] + O[t] – L[t].

Количество судов в постройке увеличивается за счет вновь заказанных судов и уменьшается за счет ввода построенных судов в эксплуатацию.

4. O[t+1] = if pos {R[t] ∙ (D[t] – N[t] – B[t])} else 0,

где R[t] – скорость принятия рыночного решения.

Количество заказанных судов есть положительная разница между спросом на них и размером заказанного и эксплуатируемого флота. Очевидно, что чем больше эта разница, тем более привлекательным выглядит решение о заказе строительства судов.

5. L[t+1] = O[t – Tbuild].

В эксплуатацию вводятся суда, заказанные Tbuild времени назад, где Tbuild – срок строительства судна.

6. S[t+1] = L[t – Tlife].

Из эксплуатации выводятся суда, отслужившие срок Tlife (срок эксплуатации судна).

Обсуждение

Строго говоря, описанные выше соотношения определяют некоторый детерминированный конечный автомат. Конечным автоматом (КА) в теории алгоритмов принято называть модель, которая может находиться только в одном из конечного числа возможных состояний в конкретный момент времени.

Автомат начинает работу в определенном начальном состоянии. В ответ на входные данные (сигналы) он изменяет свое состояние по заданному правилу, то есть осуществляет переход из текущего состояния в следующее. В отличие от так называемых «комбинационных схем», новое состояние КА зависит не только от входных сигналов, но и от текущего состояния. Детерминированный КА – автомат, в котором следующее состояние однозначно определяется текущим состоянием и входными данными, то есть переход между состояниями определен единственным образом.

При этом уравнения, используемые для описания состояний рассматриваемой модели рынка судоходства [7], определяют процессы гибели-размножения – случайные процессы, в которых переходы из текущего состояния допустимы только в соседние состояния.

При всей сложности упомянутых теоретических понятий простейшая модель без затруднений может быть реализована с помощью средств VBA MS Excel, как это показано на рисунке 1.

Рис. 1. Пример экранной формы реализации модели

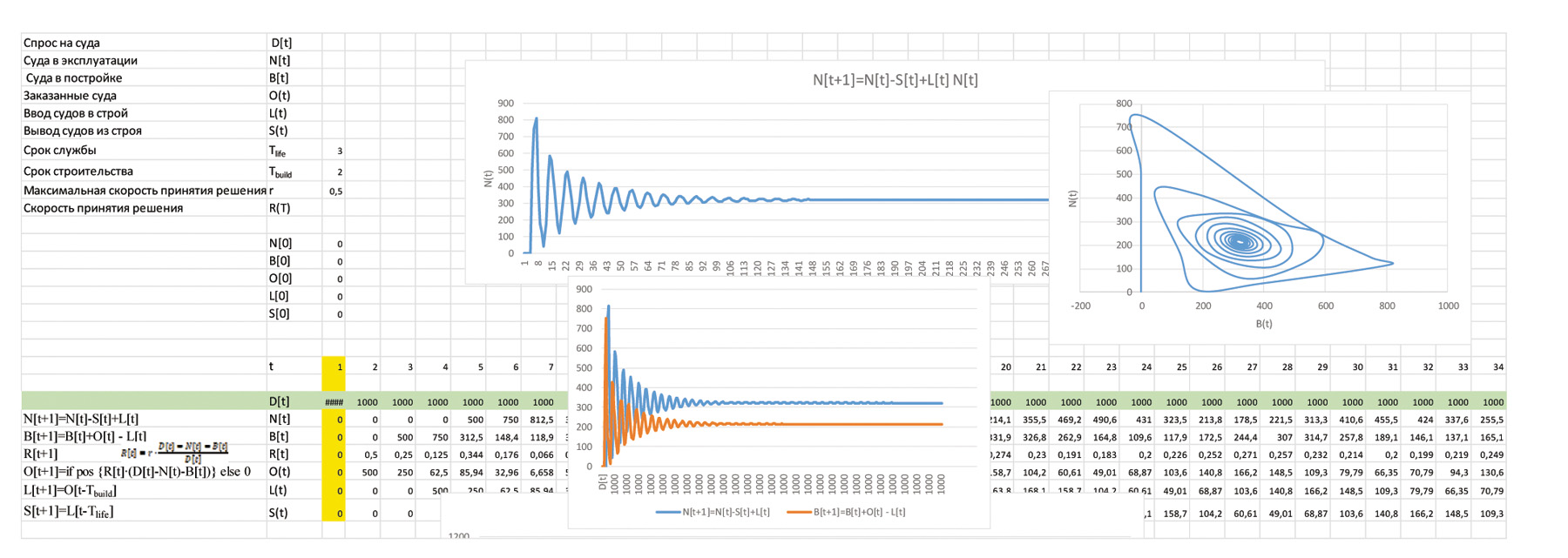
Возможны два варианта составления модели рынка судоходства: при постоянном спросе на суда, то есть D[t] = const = D0, или при произвольно меняющемся (по внешним причинам) спросе на тоннаж D[t]. Стоит отметить, что в обоих случаях при написании модели присутствует зависимость ее состояния от соотношений Tlife, Tbuild and r.

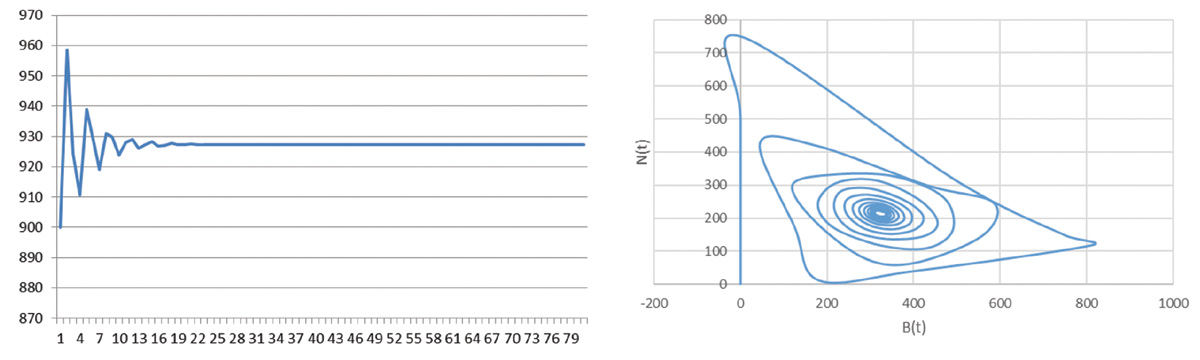
При постоянном спросе можно наблюдать классические синергетические «аттракторы» – точки «притяжения» решения к стационарному уровню, иными словами, такое состояние системы, к которому стремятся все возможные траектории ее поведения, определяемые разными начальными условиями (рис. 2).

Рис. 2. Аттрактор тоннажа

В том случае, если спрос на тоннаж произвольно меняется с течением времени, можно зафиксировать и так называемые «странные аттракторы», характеризующие более или менее стабильные колебательные процессы (рис. 3).

Рис. 3. Странный аттрактор тоннажа

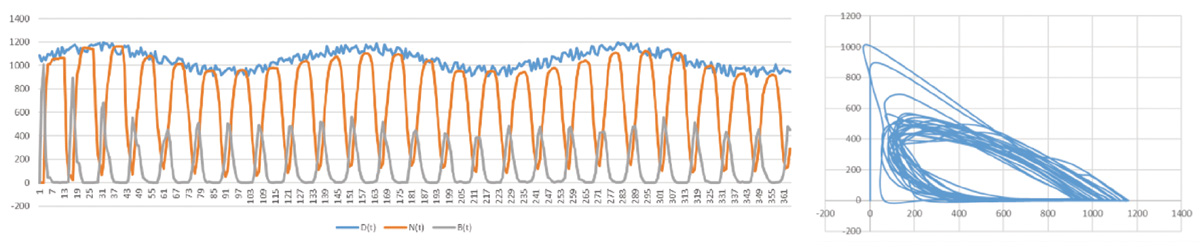
Произвольно меняющийся спрос на суда приводит к случайным колебаниям величины тоннажа на фрахтовом рынке (рис. 4). Их характер соответствует реальным данным статистики колебаний на рынке, что иллюстрирует рисунок 5.

Рис. 4. Колебания тоннажа при переменном спросе на него

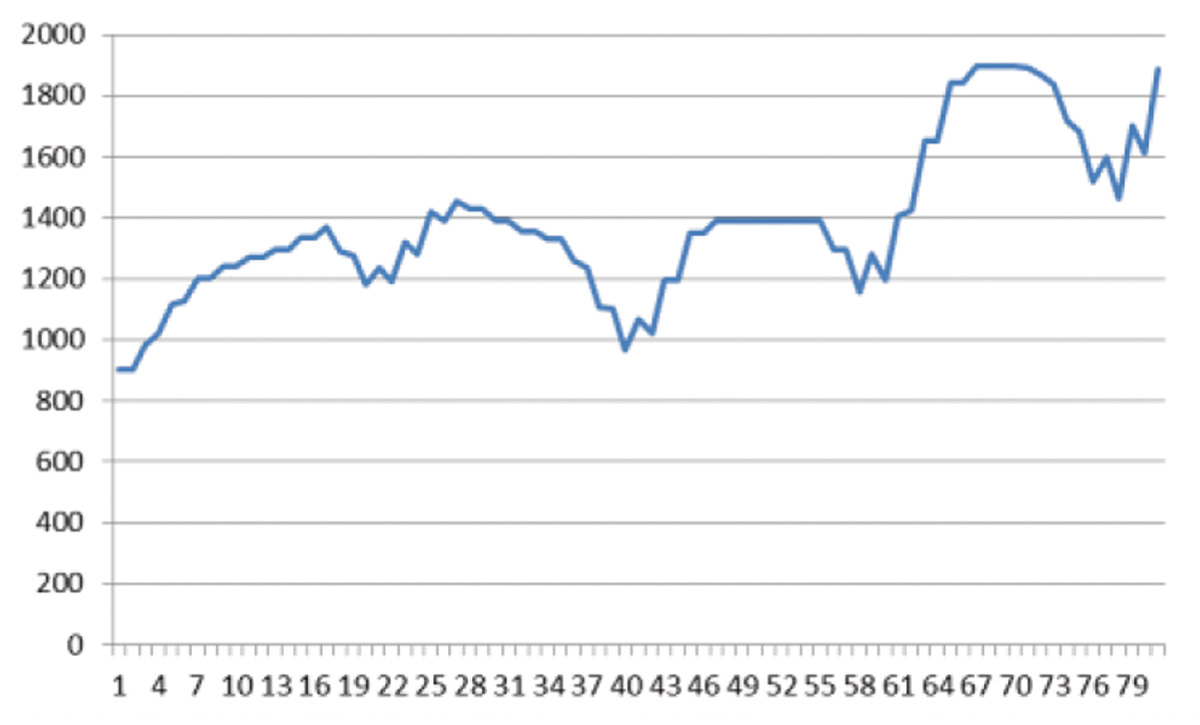
Рис. 5. Пример реальной статистики колебаний тоннажа [8]

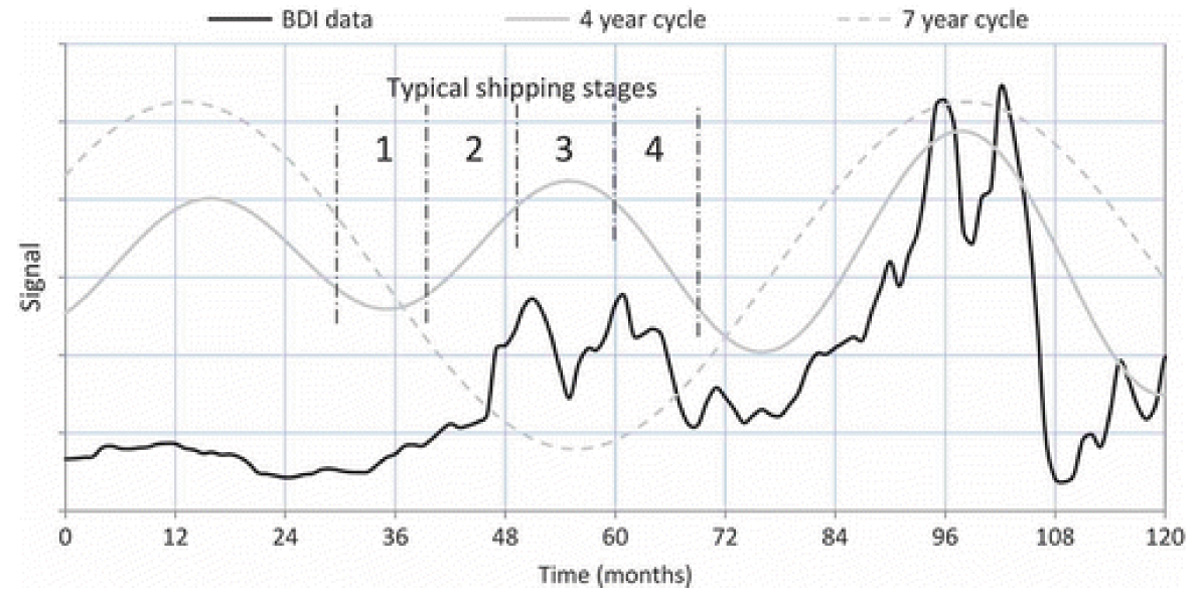
Очевидно, что любой реальный случайный процесс не может быть предсказан с точностью до деталей, и сходство в данном случае определяется, как это принято в теории математической статистики, по вероятности.

Заключение

Выявленное сходство поведения показателей позволяет предположить, что предложенная в статье упрощенная модель с достаточной степенью вероятности адекватно описывает реальную ситуацию колебаний фрахтового рынка [9]. Она позволяет проводить вполне правдоподобные начальные эксперименты по идентификации действующих на рассматриваемую динамическую систему основных факторов и установлению их относительной значимости в рамках рассматриваемой задачи.

Объяснение механизмов поведения модели, вероятно, может явиться фундаментом для прогнозирования динамики рынка. Кажущиеся на первый взгляд случайными и непредсказуемыми колебания фрахтового рынка в действительности являются синергетически устойчивыми. В то же время любые реальные прогнозы могут касаться лишь общих тенденций.

Список литературы

1. Кузнецов А.Л. Cинергетика как методологическая основа развития базовой инфраструктуры портоориентированной логистики / А.Л. Кузнецов, А.В. Галин, А.В. Кириченко // Вестник Государственного университета морского и речного флота им. адмирала С.О. Макарова.– 2016.– №6 (40).– С. 19-34.

2. Кузнецов А.Л. Прогнозирование развития морских портов на основе синергетических законов развития сложных взаимодействующих систем: монография / А.Л. Кузнецов, А.В. Галин, А.В. Кириченко – Санкт-Петербург: Изд-во ГУМФ им. адм. С.О. Макарова, 2017.– 176 с.: ил., табл.; ISBN 978-5-9509-0245-1.

3. Слицан А.Е. Структура системы «Рынок продукции морского транспорта» / А.Е. Слицан, С.А. Слицан // Эксплуатация морского транспорта. – 2006. – №2(46). – С. 3-6. – EDN HVPJFH.

4. Мамедова Л.Э.г. Мировой и внутренний грузооборот как основной фактор развития судостроительной промышленности / Л.Э.г. Мамедова, М.Е. Гоголюхина // Транспортное дело России. – 2023. – №2. – С. 117-121. – DOI 10.52375/20728689_2023_2_117. – EDN EPHGUB.

5. Слицан А.Е. Методы оценки интенсивности конкуренции на рынке продукции морского транспорта: монография / А.Е. Слицан // М-во трансп. РФ, ФГОУ ГМА им. адм. С.О. Макарова, каф. экономики и основ упр., каф. орг. и технологии перевозок. – СПб.: ГМА им. адм. С.О. Макарова, 2005. – 106 с. – ISBN 5-9509-0017-0. – EDN QQQGJL.

6. Бабурина О.Н. Мировой морской торговый флот: динамика, структура, перспективы / О.Н. Бабурина, Е.В. Хекерт, Ю.Л. Никулина // Транспортное дело России. – 2017. – №1. – С. 88-92. – EDN YICKXR.

7. Шиянская К.Ф. Стратегия и динамика фрахтового рынка в транспортно-логистической системе / К.Ф. Шиянская, А.В. Волянская // Сборник научных статей национальной научно-практической конференции профессорско-преподавательского состава ФГБОУ ВО ГУМРФ им. адмирала С.О. Макарова, Санкт-Петербург, 16 сентября 2020 года. – Санкт-Петербург: ФГБУОУ ВО ГУМРФ им. адмирала С.О. Макарова, 2020. – С. 387-390. – EDN WZSWNJ.

8. Martin Stopford Maritime economics. Second edition / USA – Routledge – 2009 – p. 815, ISBM 0415275571, 9780415275576.

9. Никифоров В.Г. Современные тенденции развития мировой судостроительной отрасли с позиции теории экономических циклов / В.Г. Никифоров, Д.С. Неслухов // Вестник Астраханского государственного технического университета. Серия: Экономика. – 2017. – №3. – С. 101-111. – DOI 10.24143/2073-5537-2017-3-101-111. – EDN ZHMWFN.

Источник:

Морские Вести России